フィボナッチ数列とアートーこの世界をデザインしたのは誰か？

こんにちはGEMMAです。突然ですがこの宇宙は
松屋の牛めしに偶然、誰かの髪の毛が入っていたように、偶然できたのでしょうか？

それとも誰かが創ったのでしょうか？偶然できたのだとすると特に論ずることはないのですが、
例えば神や超自然的エネルギー等からこの宇宙が作られたとするとどのように？が問題になってきます。
これはインテリジェント・デザイン論と言われてもいます。

今回はこの宇宙がある究極的存在によって作られていることを証明するフィボナッチ数列についてリアル解説したいと思います。

フィボナッチ数列についてみなさんは聞いたことはあるでしょうか？
これは簡単に言うと、この世界の植物や動物（クリチャー）、自然現象、人間、絵画における美の基準など多くの部分がフィボナッチという数字列をもとに設計されているというものです。

つまり、、

存在物＝フィボナッチ数列（数式）＝美の基準、が密接に関係しているということです。

これはフィボナッチ数列は中世の数学者、
レオナルド・フィボナッチ（1170ー1250）さんが発見したものです。

では前置きではなくて「美しさと数式はどう関わってくるのか」、そして「数式で世界を創った存在とは？」について考察していきます

『宇宙は我々がその言語を学び、その書かれた文字に精通するまでは読解することができない。
それらは数学的な言語で書かれていて、
その文字は三角形や円形などで創られた幾何学的図形なのである。
この言語なくして、人間にはひと言も理解できないのだ。』

17世紀の天文学者/物理学者
ガリレオ・ガリレイ

①フィボナッチ数列（ナンバー）とは？

→まずは下のビデオを見ると導入としてとてもわかりやすいです。TEDです。

１から順に隣り合う数を順に足していきます。
するとこのような数列になります。

１．１．２．３．５．８．１３．２１．３４．
５５．．．．
これがフィボナッチ数列（ナンバー）です。

このナンバーは自然界のあらゆるとこで見ることができます。

例えば、、、
花びらの数は８枚や３４枚
パイナップルの螺旋の数は５、８、１３、２１本
ひまわりの螺旋の数は２１や３４

そして上記のフィボナッチ数列を二乗していくと、、

１．１．２．３．５．８．１３．２１．３４．５５．８９．．．→

１．１．４．９．２５．６４．169．441．1156．3025．．．となり、

この二乗した数字の隣り合わせの数の和に
フィボナッチ数列が隠れていることがわかります。


また、、
二乗した数列の隣り合わせの数を足していくと、、

１＋１＋４＝６＝２x３
１＋１＋４＋９＝１５＝３x５
１＋１＋４＋９＋２５＝４０＝５x８
１＋１＋４＋９＋２５＋６４＝１０４＝８x 13

となり、この足された数字の答えを、
掛け算で表現しなおすと、、
まさに、、フィボナッチ数列が隠れていますね。

さらに！ 、、、最後の式を二乗の式で直すと、、

１＋１＋４＋９＋２５＋６４＝１０４＝８x 13
＝１²+１²＋２²＋３²＋５²＋８²＝８x１３ となります。

この数字を図形に直すと、、、
ズバリ８x１３cmの長方形のことです！

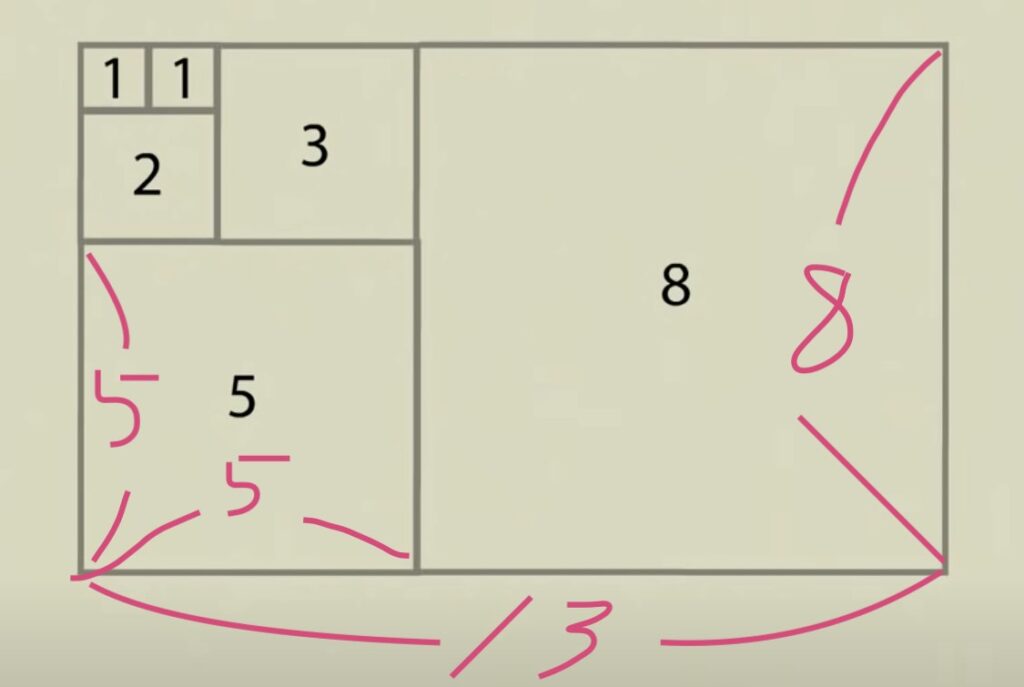
そしてこのような図形がフィボナッチによって
形成されるのですが
長辺を短編で割るとある数字が導き出されます。

８x１３ １３÷８＝１．６２５
１３x２１ ２１÷１３＝１．６１５
２１x３４ ３４÷２１＝１．６１９
３４x５５ ５５÷３４＝１．６１７６
５５x８９ ８９÷５５＝１．６１８１８

→１．６１８（黄金比）がついに導き出されます。
長方形が大くなるほど限りなく1.618に近くなっていきます。
では次に黄金比について詳しく見ていきます。

②黄金比とは？

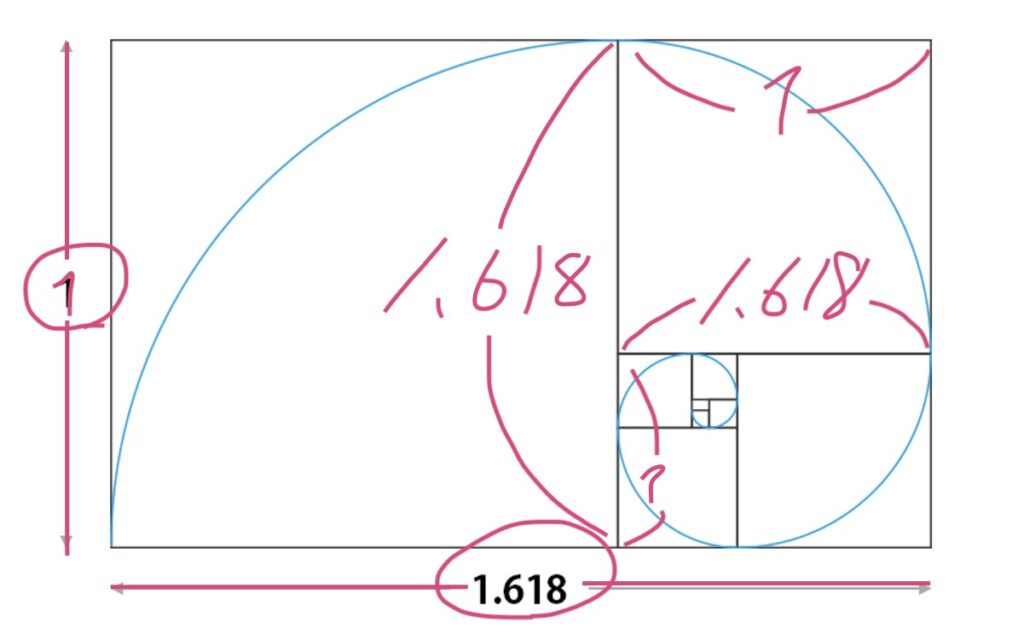
はい、これが黄金比（長さの比率が1：⒈618）
を含んだ図形です。

この図形の中に、、、

縦と横の比率が1：1.618の長方形が、、
無限と探せます。
そして長方形と長方形がくっついた部分に点を打ち、曲線で結ぶと独特の螺旋（青色）ができるんですね。これの曲線が自然界の至るところに現れています。。

つまり黄金比（数字）から出てきた螺旋の視覚的イメージです。

例えば、、、

アンモナイトの貝殻のカーブ

アンモナイトの円のカーブは等間隔で小さく
なっていくのではなく
フィボナッチの比率で徐々に小さくカーブしていきます。

またそのほかにもワラビ（蕨）の曲線にも見る
ことが出来ます。
全てが完璧なフィボナッチというわけではありません。少し揺れ幅があります。

次に、、

人体のDNA螺旋の中にも見ることができます。
これは反復するDNA螺旋の短い間隔と長い間隔の比率が黄金比率になっています。
言葉では伝わりずらいので下図を見てください。→

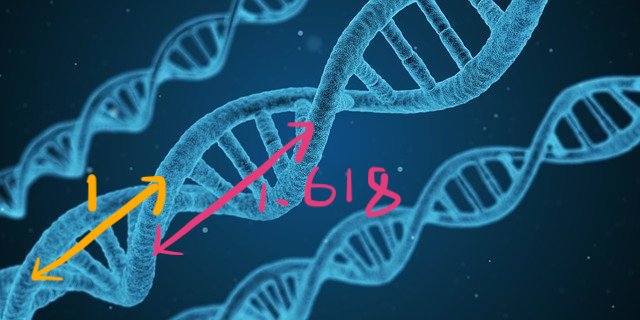
こちらDNAには反復する螺旋の間隔に短い方と、長い方がありますが
この比率が1:1.618になっていると言われています。

次に台風や銀河系の渦にも見ることができます。
これは記憶のどこかで見覚えがあるんじゃないかと思います。

これは台風の渦です、写真の角度があまりよく
ありませんが、、
著作権に引っかからない写真を探せませんでした（笑）

こちらも、、あまりいい写真ではありませんが（笑）
均等に渦を描いていくのではなくフィボナッチの比率で渦が形成されています。

③ひまわりに隠されたフィボナッチ数列

次の写真を見てみてください。

このように右回りの渦と左回りの渦をひまわりの中に確認することができます。

そして、、
これを数えると右回りが21線、左周りが34線あります。そして割ると、、、
２１➗３４＝０．６１７６
なんと０．６１７６となりフィボナッチに
関連した数字なります。
うん？（１はどこへと思うかもしれませんが、、haha）

④美術におけるフィボナッチ数列
（黄金比）

歴史を通して、多くの美術作品 の中に
フィボナッチ（黄金比）を見ることができます。
まずはこれ、ギリシャのパルテノン神殿ですね。
縦横の比率が見事に1：1.618 になっていますね。

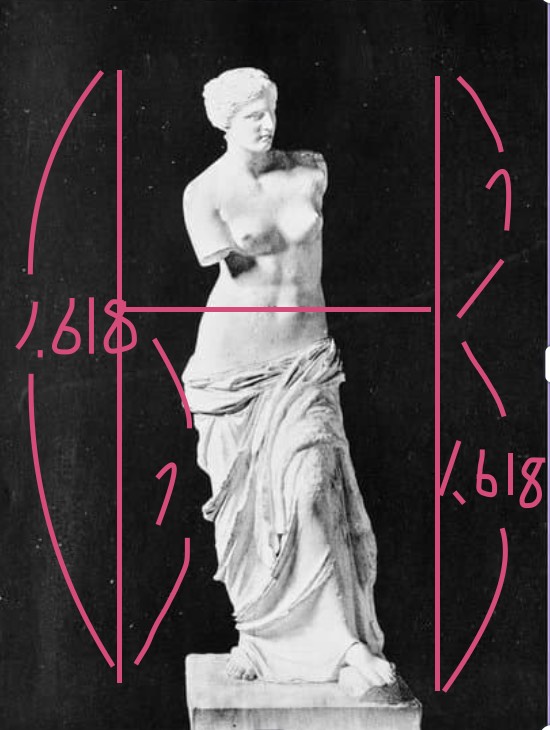
次はギリシャ彫刻のミロのヴィーナスです。
これもおへそを中心として上下が1：1.618に
なっています。
こんな昔に作られた彫刻が、、、
既にこの頃から作者は黄金比を知っていたのでしょうか？それとも、、、

次に、、ルネサンスのレオナルド・ダヴィンチの「モナリザ」です。
ここにもフィボナッチ黄金比が隠れていると言われています。

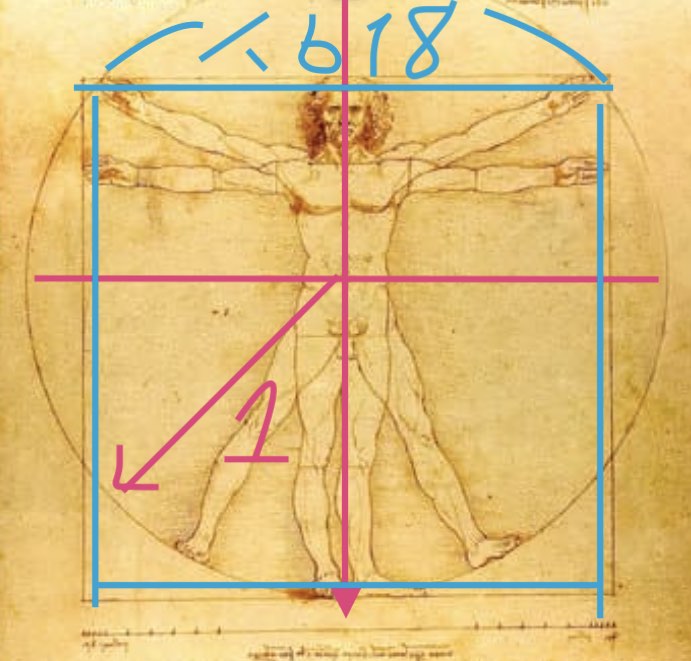
同じくダ・ヴィンチの人体比例図です。
こちらは人体のおへそを中心として
下半身の長さが１で
そこから描かれる円を囲む四角形の辺が
１．６１８の比率になっている
と言われています。

下は葛飾北斎の富嶽三十六景「神奈川沖浪裏」
です。

ここにも人間が美しいと感じるフィボナッチ螺旋を見つけることができます。
なぜ名画に黄金比を見ることができるのか、
その理由を感じれるのではないでしょうか？
そして極め付けは、、、

キャンバスのサイズです。こちらご覧ください。

これは油絵のキャンバス（Fサイズ）ですが
なんと縦横比が１：１.６１８になっています。
やはり描いた時に美しく見えるためにわざとこの規格でキャンバスを作ったのでしょう。

⑤台形に潜んだフィボナッチ数列

最後に台形に潜んでいるフィボナッチ数列を紹介します。
まだまだ山ほどあるのですが、、、、
また次の機会に、、、！

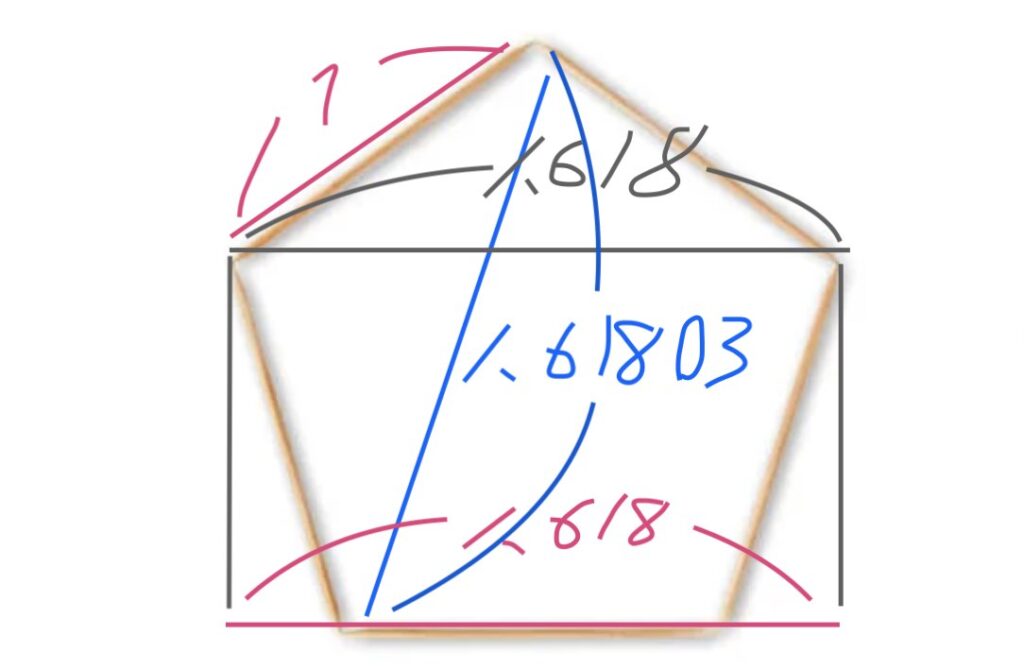
こちら台形の中にこのようにフィボナッチ数列が潜んでいます。

自然界には正五角形や正六角形が
多数存在します。

ということで自然界や芸術に含む
フィボナッチ数列と黄金比を見てきました。
美しい自然ですがその本質には数学的数字が
隠されていることが分かります。
この数字は偶然生じたとは思えません。
なぜなら偶然この世界ができたのならば
同一の数字（設計図に使われる数字）は
類似しないからです。
設計図の段階で数字と数式を決めるからこそ作品に同一の数字や数式が現れることができます。


最後にこちらの動画と聖書の句を引用します。

『神の見えない神聖、すなわち、
神の永遠の力と神聖とは、
天地創造このかた、被造物において知られていて、明らかに認められるからである。
したがって彼らには弁解の余地がない。』
聖書ローマ人への手紙第1章20節

ではまた次回お会いしましょう。
※ご意見、ご感想等あればコメント欄からお気軽に下さい。